چرخونک
علی کوچولو به تازگی یاد گرفته است خانههای زیر قطر اصلی یک جدول $n \times n$ را حذف کند و آن را $45$ درجه ساعتگرد بچرخاند. او به این شکل چرخونک تدبیر میگوید. ابتدا او در هر خانهی چرخونک یک عدد مینویسد. سپس او در هر مرحله دو خانه کهیک راس مشترک دارند و در یک ردیف افقی هستند را انتخاب میکند و مجموع آنها را به خانهی بالایشان اضافه میکند. سپس روی آن دو خانهیک ضربدر میکشد تا دیگر نتواند از آنها استفاده کند و مقدارشان را تغییر دهد. حال علی میخواهد بداند در نهایت بیشترین مقداری که خانهی بالایی چرخونک تدبیر میتواند داشته باشد چیست؟ برای مثال به شکل زیر کهیک چرخونک تدبیر $4 \times 4$ میباشد، توجه کنید.
تمام پاسخهای ارائه شده در این سوال با فرض $\Delta = 229939$ محاسبه شدهاند.
$3$- الف ($8$ نمره) : علی کوچولو چرخونک تدبیر یک جدول $7 \times 7$ را کشیده است و به سطر اول آن از پایین به ترتیب از سمت چپ نامهای $1$ تا $7$ ، به سطر دوم به ترتیب از سمت چپ نامهای $8$ تا $13$ و به خانهی بالایی آن نام $28$ را داده است. مقدار خانه $i$اٌم را با $q(i)$ نشان میدهیم و این مقدار از رابطه زیر محاسبه میشود. $$q(1) = \Delta \% 10, q(n) =(q(\lfloor n/2\rfloor) + q(n-1)+1) \% 100$$ که علامت $\%$ نشان دهنده باقیمانده میباشد. به علی بگویید بیشترین مقداری که میتواند در نهایت به خانهی بالا برساند چند است؟ اگر پاسخ این سوال برابر با $M_1$ باشد، شما باید باقیمانده $M_1$ بر $\Delta$ را به عنوان پاسخ اعلام کنید.
پاسخ
887
$3$- ب ($12$ نمره) :
فرض کنید چرخونک تدبیر یک جدول $5000 \times 5000$ باشد و مقدار خانههای آن مانند مثلث خیام-پاسکال پر شده باشد (در مثلث خیام-پاسکال اگر یک خانه همسایهی بالا چپ و بالا راست داشته باشد مقدارش برابر با جمع آنهاست و در غیر این صورت مقدارش برابر با یک میباشد). فرض کنید بیشترین مقداری که میتواند به خانهی بالا برساند برابر $M_2$ باشد، باقیماندهی $M_2$ بر $\Delta$ را حساب کنید. 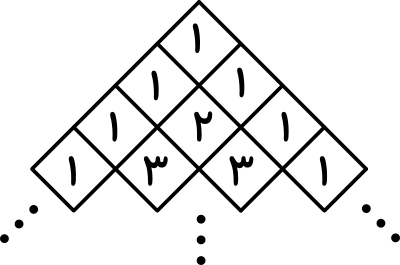
پاسخ
51200
$3$- ج ($20$ نمره) : چرخونک تدبیر یک جدول $5000 \times 5000$ که خانههای آن مانند قسمت ۱ شماره گذاری شدهاند، یعنی خانههای ردیف پایین از $1$ تا $5000$ و خانهی بالایی $\dbinom{5001}{2} $ نام گذاری شده است را در نظر بگیرید که مقدار خانهای با نام $i$ برابر $q(i)$ است . فرض کنید بیشترین مقداری که میتوان به خانهی بالا رساند برابر $M_3$ باشد باقیماندهی $M_3$ بر $\Delta$ را محاسبه کنید.
پاسخ
215973
