سوالات ۱۷ و ۱۸
یک جدولِ $6\times6$ را در نظر بگیرید که در هر خانهی آن، یک دانشآموزِ کلاسِ اول، دوم یا سوم ایستاده است. به مجموعهی دانشآموزانِ همسطر یا همستونِ یک دانشآموز (بهغیر از خودش)، سیطرهی دیدِ آن دانشآموز گفته میشود. پس سیطرهی دید هر دانشآموز، مجموعهای $10$ عضوی است.
سوال ۱۷
اگر در سیطرهی دیدِ هر دانشآموزِ کلاس اولی، حداقل یک دانشآموزِ کلاس دومی، و در سیطرهی دیدِ هر دانشآموزِ کلاس دومی، حداقل یک دانشآموزِ کلاس سومی باشد، حداکثر چند دانشآموزِ کلاس اولی میتواند در جدول وجود داشته باشد؟
- $29$
- $30$
- $35$
- $18$
- $25$
پاسخ
گزینه (1) درست است.
ابتدا با استفاده از برهان خلف اثبات میکنیم که جواب از $29$ بیشتر نیست. فرض میکنیم حداقل $30$ کلاس اولی داشته باشیم و روی تعداد کلاس دومیها حالتبندی میکنیم:
- تعداد کلاس دومیها $6$ باشد: در این حالت، جدول نمیتواند هیچ کلاس سومی داشته باشد، زیرا تمام خانهها یا کلاس اولی هستند یا کلاس دومی. بنابراین کلاس دومیها نمیتوانند وجود داشته باشند، که تناقض است.
- تعداد کلاس دومیها $5$ باشد: اگر تعداد کلاس دومیها برابر $5$ باشد، یک سطر و یک ستون وجود دارد که هیچکدام از آنها کلاس دومی ندارند. تقاطع این سطر و ستون نمیتواند کلاس اولی باشد (زیرا همه خانههای این دو شامل کلاس اولیاند)، پس این خانه حتماً باید کلاس سومی باشد. اما در این حالت، بقیهی جدول نمیتواند کلاس سومی دیگری داشته باشد (زیرا شرط مسئله نقض میشود)، ولی تعدادی کلاس دومی وجود دارند که این کلاس سومی را نمیبینند. این تناقض است.
- تعداد کلاس دومیها $4$ باشد: در این حالت، دو سطر و دو ستون وجود دارند که هیچکدام کلاس دومی ندارند. $4$ خانهای که از تقاطع این دو سطر و دو ستون حاصل میشوند، حتماً باید کلاس سومی باشند. بنابراین در مجموع حداقل $8$ کلاس دومی یا سومی در جدول وجود دارند. پس نمیتوان $30$ کلاس اولی داشت، زیرا مجموع کلاسها از $36$ بیشتر میشود.
- تعداد کلاس دومیها حداکثر $3$ باشد: در این حالت، همانند حالت قبل، حداقل $9$ خانه در جدول باید کلاس سومی باشند. بنابراین نمیتوان $30$ کلاس اولی داشت، زیرا جدول تنها دارای $36$ خانه است.
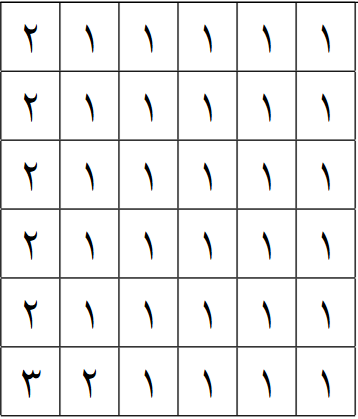
حال یک مثال از جدولی که شامل $29$ کلاس اولی، $6$ کلاس دومی، و $1$ کلاس سومی است را ارائه میدهیم:
سوال ۱۸
اگر در سیطرهی دیدِ هر دانشآموزِ کلاس اولی، تعدادِ دانشآموزانِ کلاس دومی حداقل بهاندازهی تعدادِ دانشآموزانِ کلاس اولی (در سیطرهی دیدِ او) باشد، و در سیطرهی دیدِ هر دانشآموزِ کلاس دومی، تعدادِ دانشآموزانِ کلاس سومی حداقل بهاندازهی تعدادِ دانشآموزانِ کلاس دومی باشد، حداکثر چند دانشآموزِ کلاس اولی میتواند در جدول وجود داشته باشد؟
- $18$
- $21$
- $12$
- $15$
- $19$
پاسخ
گزینه (1) درست است.
برای اثبات، ابتدا از برهان خلف استفاده میکنیم و نشان میدهیم که تعداد کلاس اولیها نمیتواند بیشتر از $18$ باشد.
فرض کنید که تعداد کلاس اولیها بیشتر از $18$ باشد. در این صورت، حداقل یک سطر و یک ستون وجود دارد که هرکدام حداقل $4$ کلاس اولی دارند. بدون کاسته شدن از کلیت مسئله، فرض کنیم این سطر و ستون، سطر اول و ستون اول باشند. حال روی خانهی تقاطع این سطر و ستون (خانهی تقاطع) حالتبندی میکنیم:
- اگر خانهی تقاطع کلاس اولی باشد: در این حالت، مجموعاً در این سطر و ستون حداقل $6$ کلاس اولی وجود دارد. از آنجا که سطر و ستون اول هرکدام $6$ خانه دارند، $5$ خانهی باقیمانده در این سطر و ستون باید کلاس دومی باشند. اما وجود $6$ کلاس دومی در این $5$ خانه ممکن نیست. بنابراین این حالت نقض فرض است.
- اگر خانهی تقاطع کلاس دومی باشد: در این حالت، در سطر یا ستون اول حداقل یک کلاس سومی وجود دارد. بدون کاسته شدن از کلیت مسئله، فرض کنیم کلاس سومی در ستون اول قرار دارد. اکنون توجه کنید که کلاس اولیهای ستون اول، در سطر خود $3$ کلاس اولی و $1$ کلاس دومی میبینند. بنابراین، در هر یک از این $4$ سطر، باید تعداد کلاس دومیها حداقل $2$ عدد بیشتر از تعداد کلاس اولیها باشد. در نتیجه، در هر کدام از این سطرها حداکثر $1$ کلاس اولی دیگر داریم. بنابراین در این $4$ سطر حداکثر $2 \times 4 = 8$ کلاس اولی وجود دارد. در دو سطر دیگر نیز حداکثر $10$ کلاس اولی وجود دارد. پس در کل حداکثر $8 + 10 = 18$ کلاس اولی وجود دارد که با فرض برهان خلف در تناقض است.
- اگر خانهی تقاطع کلاس سومی باشد: در این حالت، در ستون اول $1$ کلاس سومی و حداکثر $1$ کلاس دومی داریم. حال شرایط مشابه حالت قبلی خواهد بود. باز هم نشان میدهیم که در کل حداکثر $18$ کلاس اولی میتوانیم داشته باشیم که با برهان خلف در تناقض است.
بنابراین ثابت میشود که تعداد کلاس اولیها نمیتواند بیشتر از $18$ باشد.
مثال برای $18$: یک نمونه چیدمان برای $18$ کلاس اولی در جدول زیر آمده است: