دیرالسلطان (۲۰ نمره)
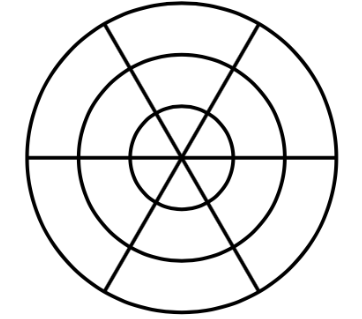
دیر السلطان شکلی است که از سه دایرهی هممرکز و $n$ قطاع تشکیل شده است. $(n \ge 3)$ برای مثال شکل زیر، یک دیر السلطان به ازای $(n=6)$ است:
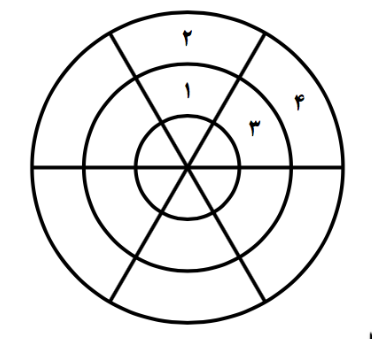
به این ترتیب یک دیرالسلطان $3n$ خانه دارد. دو خانه از یک دیرالسلطان را مجاور میگوییم اگر بیش از یک نقطه مرزی مشترک داشته باشند. برای مثال در شکل زیر، خانه ۱ با خانههای ۲ و ۳ مجاور است، ولی با خانه ۴ مجاور نیست:
آبولف و ایلیچ در حال بازی بر روی یک دیرالسلطان به ازای
$(n=1398)$
هستند. در هر مرحله آبولف یک قطاع را انتخاب میکند، طوری که آن قطاع حداقل یک خانه رنگ نشده داشته باشد. سپس ایلیچ یکی از خانههای رنگ نشده آن قطاع را انتخاب میکند. در مراحل زوج خانه انتخاب شده را آبی و در مراحل فرد خانه انتخاب شده را قرمز میکنیم. پس از آن که تمام خانه ها رنگ زده شد، بازی خاتمه مییابد.
در انتها به ازای هر دو خانه مجاور ناهمرنگ، ایلیچ باید یک واحد به ابولف پول بدهد. اگر هر دو نفر به روش بهینه بازی کنند، ایلیچ چه مقدار پول خواهد داد؟
پاسخ
ثابت میکنیم پاسخ برابر ۳*۱۳۹۸=۴۱۹۴ است.
ابتدا روشی برای سلطال ارائه میکنیم که مستقل از بازی ایلیچ بتواند دست کم ۴۱۹۴ واحد پول بگیرد. قطاعها را به ترتیب با ۱ تا ۱۳۹۸ شمارهگذاری میکنیم. سلطان در مراحل زوج، قطاعهای زوج و در مراحل فرد قطاعهای فرد را انتخاب میکند. مستقل از نحوه بازی ایلیچ، در پایان بازی هر قطاع با شماره زوج، به طور کامل آبی و هر قطاع با شماره فرد به طور کامل قرمز خواهد شد و ایلیج ۴۱۹۴ واحد پول خواهد داد.
حال روشی برای ایلیچ ارائه میکنیم که مستقل از حریف، حداکثر ۴۱۹۴ واحد پول بدهد. ایلیچ در مراح زوج، نزدیک ترین خانه ممکن به مرکز دایره و در مراحل فرد، دورترین خانه ممکن را انتخاب میکند. در این صورت در هر قطاع با حرکت از مرکز به سمت محیط، ابتدا خانههای آبی و سپس خانههای قرمز دیده خواهند شد. مقادیر زیر را برای قطاع C در نظر بگیرید:
- f(C) : تعداد زوج خانههای مجاور ناهمرنگ که هر دو خانه در C هستند.
- g(C) : تعداد زوج خانههای مجاور ناهمرنگ کهیکی در C و دیگری در قطاع بعدی در جهت ساعتگرد باشد.
مقدار پولی که ایلیچ باید بدهد برابر است با جمع $f(C)+g(C)$ به ازای تمام قطاع ها. واضح است که $f(C) \le 1$ و $g(C) \le 3$ ثابت میکنیم که $f(C)+g(C) \le 3$ و حکم مساله که ایلیچ حداکثر ۴۱۹۴ واحد پول میدهد ثابت میشود. برای ثابت کردن آن نابرابری، از برهان خلف استفاده میکنیم. فرض کنید نا برابری غلط باشد، آن گاه f(C)=1 پس قطاع دو رنگ است و g(C)=3 پس قطاع ساعتگرد بعدی دقیقا برعکس این قطاع میشود. اما طبق استراتژی ایلیچ این ممکن نیست.