دایره‌ی اعداد
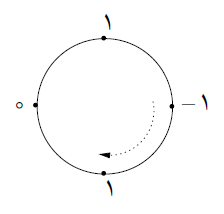
$n$ عدد حقیقی ($1 \le n$) روی یک دایره نوشته شده‌اند. مجموع این اعداد ۱ است. از یک عدد دل‌خواه روی دایره شروع می‌کنیم و به ترتیب ساعت‌گرد٬ اعداد را می‌خوانیم. $n$ عدد خوانده شده را به ترتیب در $1^3$ , $2^3$ , … و $n^3$ ضرب می‌کنیم. این $n$ عدد را باهم جمع می‌کنیم. مثلاً در شکل زیر $n=۴$ است.
اگر از عدد ۱- کار را آغاز کنیم٬ مجموع برابر
$$(-1) \times 1^3 + 1 \times 2^3 + 0 \times 3^3 + 1 \times 4^3 = 71$$
می‌شود.
نشان دهید می‌توان از عددی بر روی دایره این کار را شروع کرد که نتیجه به دست آمده بزرگتر یا مساوی $\frac{n^3}{4}$ باشد.