نقشههای درختگونه
یک نقشه شامل تعدادی شهر و جاده است به طوری که:
- هر جاده فقط دو تا از شهرها را به هم متصل میکند.
- بین هر دو شهر حداکثر یک جاده کشیده شده است.
یک نقشه درختگونه است اگر سه شرط زیر در آن برقرار باشد:
- از هر شهر آن بتوان به هر شهر دیگر از طریق جادهها مسافرت کرد.
- در صورت حذف هر کدام از جادههای نقشه، مسافرت بین دو شهر دو سر آن جاده از طریق جادههای دیگر ناممکن شود.
- تعداد جادهها دقیقا یک واحد کمتر از تعداد شهرها باشد.
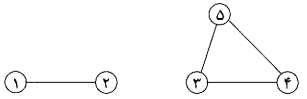
نقشهی زیر درختگونه نیست و فقط در آن شرط ۳ رعایت شده است، چون مسافرت از شهر ۱ به شهر ۳ ممکن نیست. البته در صورت حذف جادهی بین شهرهای ۳ و ۴، مسافرت بین این دو شهر از طریق شهر ۵ ممکن خواهد بود. نقشهی دوم درختگونه است.
ثابت شده است که اگر در یک نقشه دو شرط از سه شرط گفته شه درست باشد، نقشه درختگونه است و شرط دیگر هم درمورد آن صدق میکند. شما هم میتوانید این مطلب را درست فرض کنید.
در یک نقشه یک زیر مجموعه ناتهی از شهرها را درختچه مینامیم اگر بعد از حذف بقیهی شهرها و جادههای متصل به شهرهای حذف شده از نقشه، نقشهی حاصل درختگونه شود. مثلا در نقشهی زیر مجموعهی شهرهایی که با دایرهی توپر نشانهگذاری شدهاند یک درختچه است، در حالی که مجموعهی شهرهایی که با مربع توپر نشانهگذاری شدهاند درختچه نیست.
تعداد درختچههای یک نقشه را درجه استحکام آن نقشه مینامیم. بزرگترین درجهی استحکام همهی نقشههای درختگونه با n شهر را بهدست آورید.