سوال ۱۴
یک صفحه شطرنج نامتناهی داریم. برخی از خانههای این صفحه امن هستند. در هر خانه از صفحه یک عدد مینویسیم که برابر با حداقل تعداد حرکاتی است که یک مهرهی اسب باید انجام دهد تا از آن خانه به یک خانهی امن برسد. برای مثال روی خانههای امن، عدد صفر نوشته شده است.
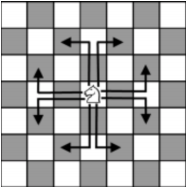
برای کسانی که با شطرنج آشنا نیستند، اگر مهرهی اسب در خانهی مشخص شدهی شکل زیر باشد، در یک گام میتواند به یکی از هشت خانهی مشخص شده برود:
فرض کنید A و B دو خانهی مجاور (دارای یک ضلع مشترک) باشند که عدد خانهی A برابر ۵۷ است. کدامیک نمیتواند عدد خانهی B باشد؟
- ۵۳
- ۵۵
- ۵۶
- ۵۷
- ۶۰
پاسخ
گزینهی ۱ درست است.
فاصلهی دو خانهی مجاور برابر سه است. پس امکان ندارد اختلاف اعداد دو خانهی مجاور بیش از سه باشد. پس پاسخ برابر ۵۳ است. برای گزینههای دیگر نیز به راحتی میتوان مثال ارائه کرد.