سوال ۲۲
درخت زیر را در نظر بگیرید. یک یال را
زرد
می‌نامیم، اگر به یک رأس درجه‌ی ۱ وصل باشد. یک رأس را
شل
می‌نامیم، اگر دست کم دو یال زرد به رئوس مسیر آن به ریشه (رأس بالا) وصل باشند (به جز یال خود رأس و یال متصل به ریشه). برای مثال $A$ در ابتدا شل است، زیرا ۴ یال زرد به رئوس مسیر آن تا ریشه وصل هستند؛ امّا رأس $B$ در ابتدا شل نیست.
در هر مرحله می‌توان یک رأس شل در نظر گرفته و از درخت حذف کرد. توجه کنید ممکن است رأسی در ابتدا شل نباشد، امّا پس از تعدادی مرحله شل شود. حداکثر چند رأس می‌توان از درخت حذف کرد؟
- ۹
- ۱۶
- ۱۰
- ۷
- ۱۳
راهنمایی
سعی کنید حذف رئوس را از راس‌هایی که ارتفاع بیشتری دارند شروع کنید.
راهنمایی
با حذف راس $A$ و دو راس هم ارتفاع و فرزند پدر $A$ شروع کنید.
راهنمایی
نشان دهید نمی‌توان رئوسی که در ارتفاع صفر، ۱ و ۲ قرار دارند را حذف کرد.
راهنمایی
در ادامه‌ی راهنمایی پیشین، سعی کنید نشان دهید سه فرزند غیر برگ ریشه را نمی‌توان با عملیات مسئله به برگ تبدیل کرد.
پاسخ
گزینه‌ی ۵ درست است.
اگر به ترتیب شماره‌های زیر، رئوس را حذف کنیم، ۱۳ رأس حذف می‌شوند:
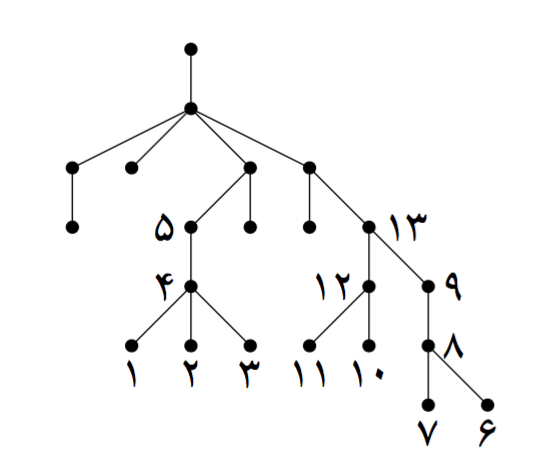حال ثابت می‌کنیم هیچ‌گاه نمی‌توان بیش از ۱۳ رأس حذف کرد. شکل زیر را در نظر بگیرید:
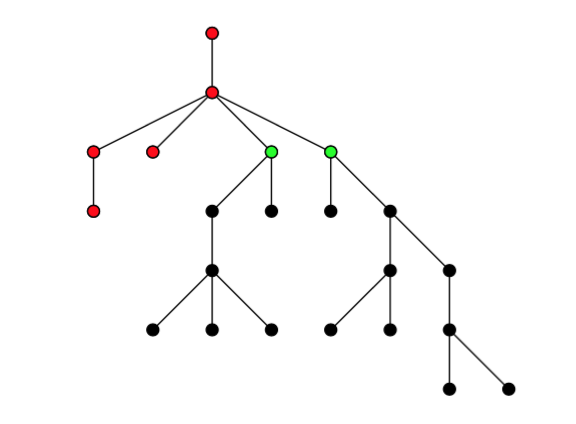رئوس قرمز و سبز و هم‌چنین دست کم یکی از دو فرزند هر کدام از رئوس سبز هیچ‌گاه حذف نمی‌شوند. این یک ناورداست (اگر در یک مرحله این حکم برقرار باشد، در مرحله‌ی بعد نیز برقرار است).
پس حداکثر ۱۳ رأس برای حذف شدن باقی می‌ماند.