سوال ۲۰
 جدولی ۵×۵ داریم. فرشید از یک خانه واقع در ستون اول شروع به حرکت میکند و در هر مرحله به سمت بالا، پایین و یا راست حرکت می کند تا نهایتا از سمت راست جدول خارج شود. او به هیچ خانه ای دو بار نمی رود و نمی تواند از بالا و پایین جدول خارج شود.
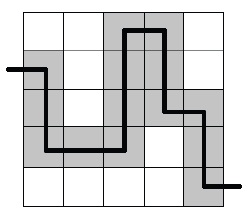
به عنوان مثال شکل مقابل یکی از مسیرهای ممکن را نشان می دهد. به ازای هر مسیری که فرشید می تواند بپیماید تعداد خانه های مسیر را یادداشت کرده ایم. مجموع این اعداد چند است؟
جدولی ۵×۵ داریم. فرشید از یک خانه واقع در ستون اول شروع به حرکت میکند و در هر مرحله به سمت بالا، پایین و یا راست حرکت می کند تا نهایتا از سمت راست جدول خارج شود. او به هیچ خانه ای دو بار نمی رود و نمی تواند از بالا و پایین جدول خارج شود.
به عنوان مثال شکل مقابل یکی از مسیرهای ممکن را نشان می دهد. به ازای هر مسیری که فرشید می تواند بپیماید تعداد خانه های مسیر را یادداشت کرده ایم. مجموع این اعداد چند است؟
- ۲۱۸۷۵۰
- ۲۰۳۱۲۵
- ۱۵۶۲۵
- ۴۳۷۵۰
- ۱۰۹۳۷۵
راهنمایی
از دوگانه شماری استفاده کنید.
راهنمایی
بجای محاسبهی مجموع طول مسیرها، میتوانید برای هر خانه تعداد مسیرهایی که شامل آن خانه هستند را حساب کنید و این مقادیر را جمع بزنید.
راهنمایی
سعی کنید حاصل جمع بیان شده در راهنمایی پیشین را برای یک ستون به شکل کامل محاسبه کنید.
راهنمایی
برای یک ستون، بخشی از مسیر که در این ستون است را در نظر گیرید. مجموع طول آن بخشها چند میباشد؟
راهنمایی
دقت کنید تعداد حالات کامل کردن یک مسیر در صورتی که بدانیم در یک ستون به چه صورت حرکت کرده، مجزا از نحوهی حرکت مسیر در آن ستون است.
پاسخ
گزینهی ۲ درست است.
برای محاسبهی جواب کافیست به جای جمع زدن طول مسیرهای ممکن، برای هر خانه تعداد مسیرهایی که از آن میگذرند را محاسبه کنیم.
یک خانه را در نظر بگیرید. برای عبور از آن باید حتما از یک سطر با شمارهی بزرگتر مساوی (یا کوچکتر مساوی) این خانه وارد ستون آن شویم و از یک سطر با شمارهی کوچکتر مساوی (یابزرگتر مساوی) این خانه از ستون آن خارج شویم.
همچنین برای حرکت بین بقیهی ستونها محدودیتی وجود ندارد و درواقع برای رفتن از یک ستون به ستون بعدی ۵ انتخاب داریم.در نتیجه در هر صورت 54 حالت برای حالات مختلف مسیر در بقیهی ستونها وجود دارد.
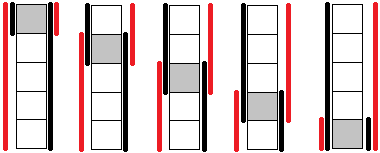
از بین 25 مسیر مختلفی که برای ورود و نهایتا خروج از این ستون وجود دارد، بسته به این که خانهی مورد نظر در کدام سطر باشد تعداد مسیرهای گذرنده از آن متفاوت خواهد بود:
- اگر در سطر اول باشد: در ۹ حالت از این خانه میگذرد.
- اگر در سطر دوم باشد: در ۱۵ حالت از این خانه میگذرد.
- اگر در سطر سوم باشد: در ۱۷ حالت از این خانه میگذرد.
- اگر در سطر چهارم باشد: در ۱۵ حالت از این خانه میگذرد.
- اگر در سطر پنجم باشد: در ۹ حالت از این خانه میگذرد.
حالات مختلف مسیر در شکل زیر مشخص شدهاند:
در نتیجه مجموع کل حالات برابر است با:
54×5×(9+15+17+15+9)=203125