سوال ۲۳
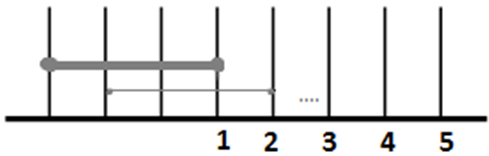
۸ میلهی عمودی مطابق شکل سمت چپ به ترتیب روی زمین چیده شدهاند٬ به طوری که فاصلهی هر میله از میلهی بعدیاش٬ برابر ۱ واحد میباشد.
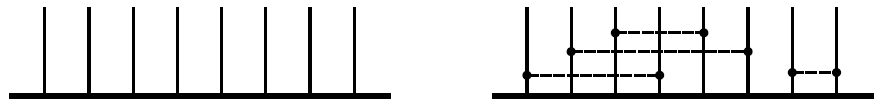
یک «جفتبندی»٬ این ۸ میله را با ۴ خطچین افقی به ۴ جفت تقسیم میکند. در شکل سمت راست یکی از راههای جفتبندی نمایش داده شده است. «طول» یک جفتبندی٬ برابر مجموع طول ۴ خطچین استفاده شده برای آن جفتبندی است. برای مثال طول جفتبندی شکل سمت راست برابر با ۱۰ میباشد. اکنون اگر همهی جفتبندیهای ممکن برای این ۸ نقطه را در نظر بگیریم٬ میانگین طول این جفتبندیها چهقدر است؟
- ۸
- ۱۲
- ۷
- ۱۶
- ۱۴
پاسخ
گزینهی (2) درست است.
تعداد همهی جفتبندیها برابر است با: \frac{\binom{8}{2} \binom{6}{2} \binom{4}{2} \binom{2}{2}}{4!}=105
تعداد دفعاتی که هر طولِ مجاز برای خطچینها، در کل جفتبندیها تکرار شدهاند را محاسبه میکنیم.
به ازای مشخص شدن طولِ یک پاره خطِ جفتکننده،\frac{\binom{6}{2} \binom{4}{2} \binom{2}{2}}{3!}=15 حالت برای کامل کردن جفتبندی وجود دارد.
میتوان خطچین به طول 1 را به 7 حالت، به طول 2 را به 6 حالت و … به طول 7 را به 1 حالت رسم کرد (شکل زیر)
پس مجموع طول جفتبندیها 1260 میشود که از رابطهی زیر به دست میآید:
(7\times1+6\times2+5\times3+4\times4+3\times5+2\times6+1\times7) \times \frac{\binom{6}{2} \binom{4}{2} \binom{2}{2}}{3!}=84\times15
و میانگین آن برابر است با: \frac{1260}{105}=12