سوال ۱۶
چند جدول ۳×۳ از اعداد ۰ تا ۸ داریم که هر دو خانهی مجاور (دارای یک ضلع مشترک) در آن دقیقاً یکی از دو خاصیت زیر را داشته باشند:
• باقیماندهی تقسیم اعداد آن دو خانه بر ۳ برابر باشد.
• خارجقسمت تقسیم اعداد آن دو خانه بر ۳ برابر باشد.
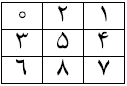
یکی از این جدولها در شکل نشان داده شده است.
- ۶
- ۱۸
- ۳۶
- ۷۲
- ۱۴۴
پاسخ
گزینهی (۴) درست است.
اگر عدد وسط 3k+x باشد 4 خانه مجاور آن’3k+x و”3k+x و3k’+x و3k”+xاست.’3k+xو ”3k+x ب به جز همین 3k+x همسایه مشترک دیگری نمیتوانند داشته باشند (چرا؟) همینطور 3k’+xو 3k”+x همسایه مشترک دیگری ندارند.’3k+x و 3k’+x دو همسایه دارند که یکی همان3k+x و دیگری’3k’+xاست. به همین ترتیب 3 جفت دیگر فقط یک همسایه مشترک دیگر دارند. پس به 4 حالت ’3k+x را در یکی از 4 خانه مجاور خانه وسط میگذاریم و ’’3k+x را به اجبار در خانهی مقابل آن میگذاریم و برای دو عدد دیگر 2 حالت داریم.اعداد 4 گوشه نیز یکتا تعیین میشوند.
پس به ازای هر عددی که وسط باشد 4×2 حالت وجود دارد و در کل 72 حالت داریم.