سوال ۱۰
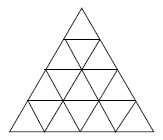 به چند طریق میتوان در ۱۶ مثلث شکل روبهرو٬ اعداد ۰ یا ۱ نوشت٬ به طوری که مجموع اعداد موجود در مثلثهای مجاور هر مثلث٬ فرد شود٬ و به چند طریق میتوان همین کار کرد که مجموع اعداد موجود در مثلثهای مجاور هر مثلث٬ زوج شود؟ (دو مثلث مجاورند اگر در یک ضلع مشترک باشند.) پاسخهای این دو سوال به ترتیب کدامند؟
به چند طریق میتوان در ۱۶ مثلث شکل روبهرو٬ اعداد ۰ یا ۱ نوشت٬ به طوری که مجموع اعداد موجود در مثلثهای مجاور هر مثلث٬ فرد شود٬ و به چند طریق میتوان همین کار کرد که مجموع اعداد موجود در مثلثهای مجاور هر مثلث٬ زوج شود؟ (دو مثلث مجاورند اگر در یک ضلع مشترک باشند.) پاسخهای این دو سوال به ترتیب کدامند؟
- ۱و ۱۶
- ۱۶ و ۱
- ۱۶ و ۱۶
- ۰ و ۱۶
- ۰ و ۱۲۸
پاسخ
گزینه (؟) درست است.
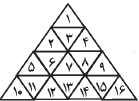 مثلثها را مطابق شکل از ۱ تا ۱۶ نامگذاری میکنیم. در حالت اول که میخواهیم مجموع اعداد موجود در مثلثهای مجاور هر مثلثی فرد باشد٬ چون تنها مثلث مجاور برای مثلث ۱ مثلث ۳ میباشد بنابراین علامت مثلث ۳ برابر «۱» میباشد. از طرف دیگر چون فقط دو خانه ۳ و ۶ مجاور خانه ۲ میباشد بنابراین علامت خانه ۶ برابر «۰» میشود. به همین ترتیب علامت خانه ۸ نیز «۰» میشود. علامت خانه ۱۳ برابر «۱» و علامت خانههای ۱۱ و ۱۵ برابر «۰» میشود که تناقض است.
مثلثها را مطابق شکل از ۱ تا ۱۶ نامگذاری میکنیم. در حالت اول که میخواهیم مجموع اعداد موجود در مثلثهای مجاور هر مثلثی فرد باشد٬ چون تنها مثلث مجاور برای مثلث ۱ مثلث ۳ میباشد بنابراین علامت مثلث ۳ برابر «۱» میباشد. از طرف دیگر چون فقط دو خانه ۳ و ۶ مجاور خانه ۲ میباشد بنابراین علامت خانه ۶ برابر «۰» میشود. به همین ترتیب علامت خانه ۸ نیز «۰» میشود. علامت خانه ۱۳ برابر «۱» و علامت خانههای ۱۱ و ۱۵ برابر «۰» میشود که تناقض است.
در حالت دوم تمام مثلثهای ۱۳٬۱۱٬۸٬۶٬۳ و ۱۵ علامت «۰» را به خود میپذیرند. هریک از دسته مثلثهای سهگانه ۲٬۱ و ۴ نیز دسته مثلثهای سه گانه ۱۴٬۹ و ۱۶ بهطور مستقل از یکدیگر به چهار طریق «۰٬۰٬۰» یا «۱٬۱٬۰» یا «۰٬۱٬۱» و یا «۱٬۰٬۱» قابل علامتگذاری میباشند و بقیه مثلثها وابسته به اینها به صورت منحصربهفرد پر میشوند٬ بنابراین طبق اصل ضرب جواب مورد نظر 4×4 میباشد.