مرتب ساز پشته ای
مرتبساز پشتهای یک مرتبساز با دو پشته است. در ابتدا در پشته اول که آن را پشته $A$ مینامیم اعداد ۱ تا $n$ با ترتیبی دلخواه قرار دارند و پشته دوم با نام $B$ خالی است. این مرتبساز قادر است عملیات زیر را انجام دهد:
- در هر مرحله دو عدد بالای پشته $A$ را در نظر میگیرد و عدد کوچکتر را به پشته $B$ انتقال میدهد و این کار را آنقدر تکرار میکند که در پشته $A$ تنها یک عنصر باقی بماند و آن را نیز به پشته $B$ منتقل میکند. سپس اعداد پشته $B$ را به پشته $A$ انتقال میدهد(توجه کنید که چون $A$ و $B$ پشته هستند ترتیب عناصر برعکس میشود) .
اگر مرتبساز پشتهای عملیات فوق را $ 1\le k\le n$ بار انجام دهد به ازای چند جایگشت اولیه از اعداد ۱ تا $n$ درون $A$ ، در نهایت اعداد بصورت مرتب شده در پشته $A$ قرار خواهند گرفت (عدد ۱ در بالای پشته و عدد $n$ در پایین پشته). جواب را بر حسب $n$ و $k$ محاسبه و اثبات کنید.
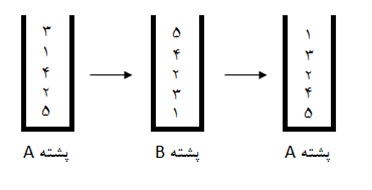
به عنوان مثال در شکل زیر وضعیت پشته $A$ بعد از یک بار انجام عملیات نمایش داده شده است. در این شکل سه گام مشخص شده است که به ترتیب عبارتند از: وضعیت اولیه پشته $A$ ، نحوه قرار گرفتن اعداد در پشته $B$ ، وضعیت اعداد در پشته $A$ بعد از عملیات.
پاسخ
مشاهده۱: تبدیل مسئلهی پشته به مسئلهی آرایه:
عملیات گفته شده مانند این است که یک آرایه از اعداد $a_1, a_2, …, a_n$داشته باشیم. سپس از دو عنصر اول آرایه یعنی $a_1$ و $a_2$شروع کنیم و آن دو را با هم مقایسه کنیم. اگر $a_1$ بزرگتر بود جای آن دو را با هم عوض کنیم. سپس به سراغ دو عنصر بعدی برویم و همینطور تا آخرین دو عنصر آرایه، این کار را انجام دهیم. هدف این است که در انتها آرایه مرتب شود. یعنی: $a_1<= a_2<= … <= a_n$
نکته خارج از راهحل: درواقع این عملیات، بخشی از مرتبسازی حبابی است. در مرتبسازی حبابی با $n$ بار انجام این عملیات مطمئن میشویم که آرایه مرتب شده است.
با توجه به مشاهده۱ کافی است ببینیم که به ازای چه آرایههایی از اعداد ۱ تا $n$، با $k$ بار انجام دادن عملیات بالا، در انتها به یک آرایهی مرتب شده میرسیم.
لم۱: اگر در آرایهی $A$ با عناصر $a_1, a_2, …, a_n$ که جایشگتی از اعداد ۱ تا $n$ هستند، شرط زیر برقرار باشد، با $k$ بار انجام دادن عملیات مذکور در مشاهده۱، دنباله مرتب میشود و در غیر این صورت دنباله در انتها نامرتب خواهد بود:
- به ازای هر $۱≤i≤n$، تعداد اعدادیکه بیشتر از $a_i$ هستند و در آرایه قبل از آن قرار دارند، حداکثر $k$ باشد.
اثبات: در ابتدا نشان میدهیم درصورتی که شرط گفته شده برقرار نباشد، در انتها جایگشت مرتبشده نخواهد بود. فرض کنید قبل از $a_i$ بیشتر از $k$ عدد باشند که از آن بیشتر هستند. در هر بار اجرای عملیات بالا، حداکثر یکی از این اعداد از $a_i$ رد میشود و بعد از آن قرار میگیرد. بنابراین در انتها حداقل یکی از آنها قبل از $a_i$ باقی میماند و بنابراین جایشگت مرتب نمیشود.
حال نشان میدهیم درصورتی که شرط گفته شده برقرار باشد، در انتها دنباله مرتب میشود. این فرض را با استقرا روی $n$ نشان میدهیم.
حالت پایه: وقتی است که $n=1$ که مرتب است.
گام استقرا:
عدد ۱ را در دنباله در نظر بگیرید. با توجه به شرط لم، حداکثر $k$ عدد دیگر قبل از عدد یک قرار دارند. از طرفی چون عدد یک، کوچکترین عدد دنباله است، در هر مرحله جایگاهاش یک واحد به سمت چپ انتقال پیدا میکند تا وقتی که به سمت چپترین نقطه برسد. بنابراین بعداز $k$ مرحله، عدد یک در جایگاه درست قرار میگیرد.
حال اگر عدد یک را در نظر نگیریم، بقیهی اعداد مستقلا باید شرط لم را داشته باشند (چون عدد یک کوچکترین عدد است). از طرفی جایگاه عدد یک در ترتیب مقایسهی این اعداد تاثیری ندارد. بنابراین طبق فرض استقرا اگر روی آنها $k$ مرحله عملیات گفته شده را انجام دهیم مرتب میشوند. بنابراین بعداز $k$ مرحله کل دنباله مرتب خواهد شد.
قضیه: تعداد جایگشتهایی که با $k$ بار انجام عملیات گفته شده$(k≤n)$ قابل مرتب شدن هستند، برابر است با $k!\times (k+۱)^{n-k}$.
اثبات:
اثبات را با استقرا روی $n$ انجام میدهیم:
پایه: $n=k$. در این صورت با توجه به لم۱ همهی جایشگتها قابل مرتب شدن هستند.
گام استقرا: برای اینکه دنباله مرتب شود باید شرط لم۱ را داشته باشد. از طرفی با حذف عدد یک از دنباله، دنبالهای که باقی میماند، مستقل از عدد یک باید همچنان شرط لم۱ را داشته باشد. بنابراین بدون در نظر گرفتن عدد یک، $n-1$ عدد داریم که طبق فرض استقرا $k!\times (k+1)^{n-1-k}$ جایگشت از آنها قابل مرتب شدن هستند. حال به ازای هر جایگشت، برای اینکه شرط لم۱ برقرار بماند، دقیقا $k+1$ حالت برای اضافه کردن عدد یک وجود دارد. پس در کل $k!\times(k+1)^{n-k}$ جایگشت قابل مرتب شدن هستند.