سوال ۳۸
چند دنبالهی $a_1,a_2,...,a_13$ از اعداد ۱ تا ۱۳ وجود دارد که هر عدد دقیقا یک بار در آن ظاهر شده باشد و نیز $a_i$ از $a_{3i-1}$ و $a_{3i+1}$ کوچک تر باشد؟
- $ {\binom{12}{4}}^2 \times 6^3$
- $ {\binom{13}{9}}^2 \times 3^3$
- $ {\binom{12}{4}}^2$
- $3^3 \times 24$
- $ {\binom{13}{9}}^2$
پاسخ
گزینه (؟) درست است.
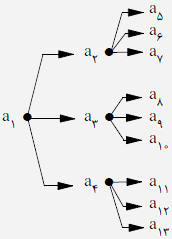
باید درخت موجود در شکل زیر را تکمیل کنیم(« » نشانگر آن است که عدد $x$ از عدد $y$ کوچکتر است).
» نشانگر آن است که عدد $x$ از عدد $y$ کوچکتر است).
عدد $a_1$ کوچکترین عدد ممکن یعنی ۱ میباشد. حال ۱۲ عدد باقیمانده را به سه دستهی چهار تایی تقسیم میکنیم تا به شاخههای $a_1$ اختصاص دهیم که این کار به $\binom{12}{4} \binom{4}{8} \binom{4}{4}$ طریق ممکن است. در بین دستهی اول کوچکترین عدد را به $a_2$ و سه عدد دیگر را به $3!$ طریق بین $a_5$ و $a_6$ و $a_7$ تقسیم میکنیم. دستههای دیگر را نیز به همین صورت بین $a_i$ های باقیمانده تقسیم میکنیم٬ بنابراین جواب مورد نظر برابر $\binom{12}{4} \binom{4}{8} \times (3!)^3$ خواهد شد که جواب صحیح در بین گزینههای نیامده است.