روبیک اعداد
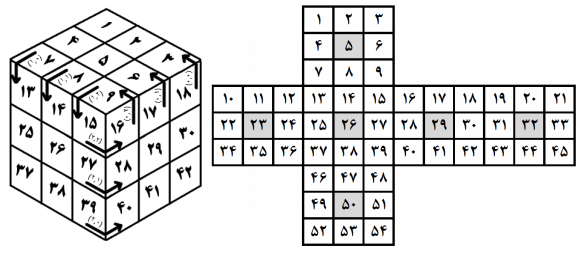
هوشنگ که از خورههای روبیک است، جدیدا با «روبیک اعداد» آشنا شده است. تنها تفاوت روبیک اعداد با روبیک عادی این است که خانههایش به جای رنگ، با اعداد پر شدهاند. یک نمونه از روبیک اعداد و همچنین حالت باز شدهی آن در زیر آمده است.
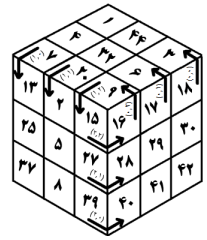
در حالت باز شده، خانههای $5$، $23$، $26$، $29$، $32$ و $50$ به ترتیب خانههای مرکزی وجههای بالا، چپ، جلو، راست، عقب و پایین مکعب هستند. همانطور که در شکل بالا نیز مشخص شده است، $9$ حرکت بر روی این مکعب مجاز است که هر کدام از حرکات یکی از لایههای مکعب را در جهت مشخص شده روی شکل، $90$ درجه میچرخاند. حرکات با یک جفت از اعداد مانند $(a,b)$ ($0\leq a,b \leq 2$) مشخص شدهاند. برای مثال اگر یکبار حرکت $(1,1)$ انجام شود، وضعیت زیر بدست میآید.
ارزش یک وضعیت از روبیک اعداد با فرمول $\sum_{i=1}^{54} (i - p_i)^4$ مشخص میشود که $p_i$ نشاندهندهی عددی است که بر روی خانهی $i$ نوشته شده است. برای مثال در حالت اولیه، به ازای تمامی $i$ها، $p_i=i$ است. دقت کنید که حق چرخاندن روبیک در فضا را نداریم و تنها میتوانیم لایهها را با همان جهتی که مشخص شده، بچرخانیم.
هوشنگ از شما خواسته است که با شروع از حالت اولیه، دنبالهای از حرکات را که در سوالات زیر شرح داده شدهاند، انجام دهید و سپس ارزش وضعیت نهایی بعد از انجام حرکات را حساب کنید. برای ساختن دنبالهی حرکات، از تابع $d(i)$ استفاده میشود. تابع $d(i)$ برابر با باقیماندهی تعداد مقسومعلیههای عدد $i$ بر $3$ است.
تمام پاسخهای ارائه شده در این سوال با فرض $\Delta = 10007$ محاسبه شدهاند.
$5$- الف ($10$ نمره) : اگر $100$ حرکت انجام دهیم و حرکت $i$ ام برابر $(0,d(i))$ باشد، باقیماندهی ارزش وضعیت نهایی بر $\Delta$ چند است؟
پاسخ
2993
$5$- ب ($12$ نمره) : اگر $100$ حرکت انجام دهیم و حرکت $i$ ام برابر $(d(i),1)$ باشد، باقیماندهی ارزش وضعیت نهایی بر $\Delta$ چند است؟
پاسخ
2376
$5$- ج ($16$ نمره) : اگر $10000$ حرکت انجام دهیم و حرکت $i$ ام برابر $(d(2i),d(2i+1))$ باشد، باقیماندهی ارزش وضعیت نهایی بر $\Delta$ چند است؟
پاسخ
1097