گراف خیام-پاسکال
گراف خیام-پاسکال از روی مثلث خیام-پاسکال به صورت زیر ساخته میشود. به ازای هر خانه از مثلث خیام-پاسکال مانند $\binom{n}{k}$ ، یک راس در گراف در نظر گرفته میشود. دو راس $\binom{n_1}{k_1}$ و $\binom{n_2}{k_2}$ به یکدیگر متصل هستند، اگر یکی از شرایط زیر برقرار باشد:
- $n_1=n_2, | k_1 - k_2 | = 1$
- $n_2=n_1+1, k_1\leq k_2\leq k_1+1$
- $n_1=n_2+1, k_2\leq k_1\leq k_2+1$
در این صورت هر راس، حداکثر $6$ همسایه خواهد داشت.
گراف $G(R)$، شامل تمامی راسهایی مانند $\binom{n}{k}$ است که مقدار $\binom{n}{k}$ زوج و $n < R$ است. دو راس در $G(R)$ به یکدیگر متصل هستند اگر و فقط اگر در گراف خیام-پاسکال به یکدیگر متصل باشند.
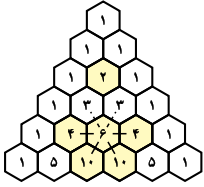
شکل زیر $6$ سطر اول مثلث خیام-پاسکال را نشان میدهد. راسهای گراف $G(6)$ در این شکل، با پسزمینهی رنگی مشخص شدهاند. یالهای متصل به راس $\binom{4}{2}$ نیز در گراف مشخص شدهاند. یالهایی که در گراف $G(6)$ هستند، با خط ممتد و یالهای خارج از آن، با خطچین نمایش داده شدهاند.
تمام پاسخهای ارائه شده در این سوال با فرض $\Delta = 10007$ محاسبه شدهاند.
$4$- الف ($11$ نمره) : اگر $X$ نشاندهندهی تعداد مولفههای همبندی گراف $G(2^{20})$ باشد، باقیماندهی $X^2$ بر $\Delta$ چند است؟
پاسخ
1932
$4$- ب ($11$ نمره) : اگر $X$ نشاندهندهی تعداد مولفههای همبندی گراف $G(1020304050)$ باشد، باقیماندهی $X^2$ بر $\Delta$ چند است؟
پاسخ
7574