اعداد زیبا
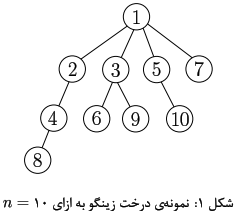
زینگو یک درخت ریشهدار $n$ راسی دارد که راسهای آن با اعداد $1,2,\ldots,n$ شمارهگذاری شدهاند. در این درخت شمارهی راس ریشه برابر با $1$ است و شمارهی پدر راس $i>1$ برابر با بزرگترین مقسومعلیه عدد $i$ است که از $i$ کوچکتر است. $f(i)$ را برابر با تعداد راسهایی که پدرشان راس $i$ است تعریف میکنیم. زینگو میتواند به تعداد دلخواه هر یک از دو عملیات زیر را برروی راسهای این درخت با شمارهی $i>1$ انجام دهد:
- در صورتی که زیبا باشد و راس $i$ فرزندی نداشته باشد، میتواند راس $i$ را از درخت حذف کند و در سبد خود قرار دهد. این عملیات هزینهای ندارد.
- پدر راس $i$ را به راس دیگری که همچنان در درخت باقیمانده است و در زیردرخت راس $i$ نیست، تغییر دهد. این عملیات یک واحد هزینه دارد.
هدف زینگو این است که بیشترین تعداد راسهایی که شمارهی آنها زیبا است را با صرف کمترین هزینه در سبد خود قرار دهد. اگر زینگو بتواند با $k$ واحد پول، حداکثر $x$ تا از راسها را در سبد خود قرار دهد و برای این کار به حداقل $y$ واحد پول نیاز داشته باشد، در این صورت قرار میدهیم $A_k=x \times y$.
تمام پاسخهای ارائه شده در این سوال با فرض $\Delta = 10289$ محاسبه شدهاند.
$2$- الف ($9$ نمره) : اگر $n=40000$ باشد و اعدادی که سه مقسومعلیه دارند زیبا باشند، باقیماندهی $\sum_{k=1}^{150}A_k^2$ بر $\Delta$ چند است؟
پاسخ
706
$2$- ب ($8$ نمره) : اگر $n=10^6$ باشد و اعدادی که دو مقسومعلیه دارند زیبا باشند، باقیماندهی $\sum_{k=1}^{250000}A_k^2$ بر $\Delta$ چند است؟
پاسخ
679
$2$- ج ($16$ نمره) : اگر $n=10^6$ باشد و اعدادی که سه یا چهار یا پنچ مقسومعلیه دارند زیبا باشند، باقیماندهی $\sum_{k=1}^{250000}A_k^2$ بر $\Delta$ چند است؟
پاسخ
2743
توجه: دقت کنید که بعنوان مثال عدد $6$ دارای $4$ مقسومعلیه و عدد $25$ دارای $3$ مقسومعلیه میباشد.