فهرست مندرجات
سوالات ۱۲ و ۱۳ و ۱۴
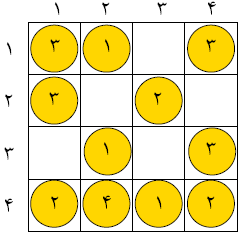 یک جدول $۱۶\times ۱۶$ را در نظر بگیرید که سطرها و ستونهای آن به ترتیب شمارههای ۱ تا ۱۶ گرفتهاند. هر خانه میتواند خالی باشد یا درون آن یک سکه قرار گرفته باشد. روی هر سکه یک شماره بین ۱ تا ۱۶ نوشته شده است٬ اما از هر شماره حداکثر ۱۶ سکه در جدول وجود دارد. در شکل روبهرو مثالی از یک جدول $۴\times ۴$ با ۱۱ سکه دیده میشود. توجه کنید که برای سادگی٬ دو شکل اول برای جدول $۴\times ۴$ رسم شدهاند. اما هر سه سوال را باید براساس جدول $۱۶\times ۱۶$ پاسخ دهید.
یک جدول $۱۶\times ۱۶$ را در نظر بگیرید که سطرها و ستونهای آن به ترتیب شمارههای ۱ تا ۱۶ گرفتهاند. هر خانه میتواند خالی باشد یا درون آن یک سکه قرار گرفته باشد. روی هر سکه یک شماره بین ۱ تا ۱۶ نوشته شده است٬ اما از هر شماره حداکثر ۱۶ سکه در جدول وجود دارد. در شکل روبهرو مثالی از یک جدول $۴\times ۴$ با ۱۱ سکه دیده میشود. توجه کنید که برای سادگی٬ دو شکل اول برای جدول $۴\times ۴$ رسم شدهاند. اما هر سه سوال را باید براساس جدول $۱۶\times ۱۶$ پاسخ دهید.
با توجه به توضیح بالا به سه سوال زیر پاسخ دهید:
سوال ۱۲
در یک سطر دلخواه٬ حداکثر چند سکه ممکن است وجود داشته باشد که عدد نوشته شده بر روی آنها برابر باشد؟ (در مثال بالا این عدد ۲ است)
- ۸
- ۱
- ۲
- ۴
- ۱۶
پاسخ
گزینهی (۵) درست است.
همهی سکههای با یک شماره میتوانند در یک ردیف باشد. در نتیجه جواب برابر ۱۶ است.
سوال ۱۳
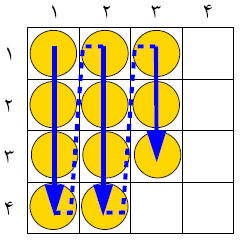 فرض کنید که تمام سکههای این جدول را برمیداریم و براساس عدد نوشته شده بر روی آنها به صورتی که در شکل نشان داده شده است به صورت مرتب میچینیم. در این نحوهی مرتبسازی سکهها از خانهی (۱٫۱) تا (۱۶٫۱۶) مطابق شکل دنبال هم فرض میشوند (توجه کنید سکهی واقع در (۱٫۲) پس از سکهی واقع در (۱۶٫۱) فرض میشود. منظور از (۱٫۲) خانهي سطر ۱ و ستون ۲ است.) با این مرتبسازی سکههایی که عددشان برابر است پشت سرهم قرار میگیرند.
فرض کنید که تمام سکههای این جدول را برمیداریم و براساس عدد نوشته شده بر روی آنها به صورتی که در شکل نشان داده شده است به صورت مرتب میچینیم. در این نحوهی مرتبسازی سکهها از خانهی (۱٫۱) تا (۱۶٫۱۶) مطابق شکل دنبال هم فرض میشوند (توجه کنید سکهی واقع در (۱٫۲) پس از سکهی واقع در (۱۶٫۱) فرض میشود. منظور از (۱٫۲) خانهي سطر ۱ و ستون ۲ است.) با این مرتبسازی سکههایی که عددشان برابر است پشت سرهم قرار میگیرند.
پس از انجام این مرتبسازی٬ در یک سطر دلخواه حداکثر چند سکه ممکن است وجود داشته باشد که عدد نوشته شده بر روی آنها برابر باشد؟ (در جدول مثال اولیه٬ این عدد ۱ است)
- ۱
- ۸
- ۷
- ۲
- ۴
پاسخ
گزینهی (۱) درست است.
تمام سکهها با عدد برابر پشت سر هم قرار دارند. برای اینکه دو تا از آنها در یک سطر باشند باید بین آنها ۱۵ سکه وجود داشته باشد که چون از هر عدد ۱۶ سکه داریم چنین چیزی ممکن نیست. پس در یک سطر هیچ دو سکهی یکسانی وجود ندارد.
سوال ۱۴
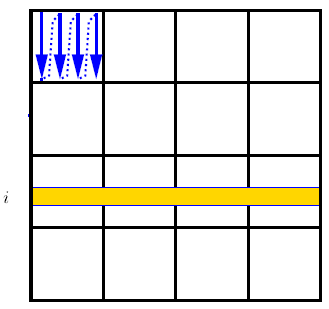
فرض کنید که جدول اولیه را مطابق شکل زیر به ۱۶ جدول هریک به اندازهی $۴\times ۴$ تقسیم میکنیم. اگر سکههای موجود در هریک از این جدولهای کوچکتر $۴\times ۴$ را (مستقل از بقیهی جدولها) مطابق مسئلهی قبل درون خود آن جدولها مرتب کنیم٬ حال در یک سطر دلخواه٬ حداکثر چند سکه ممکن است وجود داشته باشد که عدد نوشته شده بر روی آنها برابر باشد؟
- ۲
- ۴
- ۱
- ۷
- ۸
پاسخ
گزینهی (۴) درست است.
اگر در ۱۶ خانهی اول، ۱۶ خانهی دوم و ۱۶ خانهی سوم ۵ سکه با شمارهی یک و در ۱۶ خانهی چهارم یک سکه با شمارهی یک داشته باشیم در ردیف اول ۷ عدد سکه با شماره یک قرار میگیرد.
در یک قسمت ۴×۴ جدول اگر بخواهیم حداکثر تعداد سکههای یکسان در یک ردیف یک باشد حداقل یک سکه، اگر بخواهیم این مقدار ۲ باشد حداقل به ۵ سکه و در کل اگر بخواهیم این مقدار $i$ باشد به$4i-3$ سکه یکسان نیاز داریم. حال اگر بخواهیم ۸ عدد سکهی یکسان در یک ردیف داشته باشیم ابتدا در هر ۴×۴ یک سکه قرار میدهیم. از این به بعد برای اضافه کردن یک واحد به تعداد حداکثر سکههای موجود در یک سطر باید این مقدار را برای یکیاز ۴×۴ها زیاد کنیم.
یعنی برای هر واحد زیاد کردن آن به ۴ سکه نیاز داریم و چون ۱۲ سکه دیگر داریم این مقدار به ۸ نمیرسد.

