فهرست مندرجات
CRYPTO
موضوع امنیت در اینترنت یکی از مهمترین موضوعهای مورد مطالعهی سالهای اخیر است. یکی از روشهای امنیت، رمزنگاری دادهها است. الگوریتم «پفکی»، یکی از پرکابردترین روشها برای رمزنگاری است. این الگوریتم برای رمزنگاری دادهها، از دو دنبالهی $a_0,a_1,\cdots,a_{n-1}$ و $b_0,b_1,\cdots,b_{m-1}$ استفاده میکند. میزان امنیت الگوریتم «پفکی» با استفاده از روش زیر قابل محاسبه است:
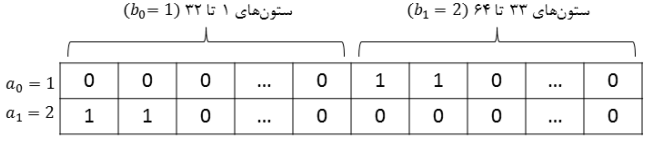
«جدولی با $n$ سطر و $32\times m$ ستون در نظر بگیرید که در خانهی $(i,j)$ $(0\leq i\leq n-1, 0\leq j\leq 32\times m-1)$ از آن $\mathrm{getBit}(a_i \oplus b_{\lfloor \frac{j}{32} \rfloor}, j \mod 32)$ نوشته شده است. در اینجا تابع $\mathrm{getBit}(x,p)$ بیت $p$ ام از عدد $x$ را برمیگرداند، برای مثال $\mathrm{getBit}(6,0)=0$ ، $\mathrm{getBit}(6,1)=1$ و $\mathrm{getBit}(6,2)=1$ هستند. تمام جدولهایی که از جدول ساخته شده با جابهجایی ستونها میتوان ساخت را در نظر بگیرید (حداکثر $32m!$ جدول متفاوت) و به ازای هر کدام از این جدولها اندازهی بزرگترین زیرجدولی (بزرگترین از لحاظ تعداد خانههای تشکیل دهنده) که تمام خانههایش $1$ است را محاسبه کنید. بیشینهی اعداد محاسبه شده برابر با میزان امنیت الگوریتم پفکی به ازای ورودیهای $a_0,a_1,\cdots,a_{n-1}$ و $b_0,b_1,\cdots,b_{m-1}$ است. دقت کنید که تنها جابهجایی ستونها مجاز است و جابهجایی سطرها مجاز نیست.»
شما باید برنامهای بنویسید که با توجه به ورودیهای الگوریتم پفکی، میزان امنیت آن را مشخص کند.
علامت $\oplus$ نشاندهندهی عملگر $\mathrm{xor}$است. عبارت $a\mod b$ نیز نشاندهنده باقیمانده عدد $a$ بر $b$ است.
ورودی
در سطر اول ورودی به ترتیب دو عدد طبیعی $n$ و $m$ آمده است.
در سطر دوم $n$ عدد صحیح آمده است که عدد $i$ ام $(1\leq i\leq n)$ آن نشاندهندهی $a_{i-1}$ است.
در سطر سوم $m$ عدد صحیح آمده است که عدد $i$ ام $(1\leq i\leq m)$ آن نشاندهندهی $b_{i-1}$ است.
خروجی
در تنها سطر خروجی میزان امنیت روش پفکی را به ازای دنبالههایی که در ورودی آمده است، چاپ کنید.
زیرمسئلهها
- زیرمسئله اول (۲۲ نمره): $n,m\leq 700$
- زیرمسئله دوم (۵۵ نمره): $n,m\leq 2\times 10^5$
- زیرمسئله سوم (۲۳ نمره): بدون محدودیت اضافی
محدودیتها
- $1\leq n,m\leq 10^6$
- $0\leq a_i, b_i < 2^{30}$
ورودی و خروجی نمونه
| ورودی نمونه | خروجی نمونه |
|---|---|
| 2 2 1 2 1 2 | 2 |
| 4 4 1 3 2 10 4 1 7 15 | 16 |
شرح ورودی و خروجی نمونه
جدول حاصل از ورودی نمونهی اول در شکل زیر نشان داده شده است. تمام خانههای ستونهایی که با سهنقطه مشخص شدهاند، حاوی عدد 0 هستند. با توجه به جدول هر طوری ستونها را جابهجا کنیم زیرجدولی تمام $1$ با اندازهی بیشتر از $2$ نخواهیم داشت. بنابراین پاسخ مسئله همان $2$ است. لازم به ذکر است که در جدول اولیه هم اندازهی بزرگترین زیرجدول تمام $1$ برابر $2$ است.