فهرست مندرجات
Kunai
کونای یک اسلحهی تیز مورد استفادهی نینجاها است که شکلی شبیه به چاقو دارد. نینجاها با پرتاب کونایها بهسمت دشمنانشان با آنها میجنگیدند.
در یک جدول با $W$ ستون و $H$ سطر از خانههای مربعشکل، $N$ نینجا قرار دارند. هر نینجا در مرکز یک خانه قرار دارد، و هیچ دو نینجایی در یک خانهی مشترک نیستند. هر نینجا یک کونای دارد، و به سمت یکی از چهار جهت اصلی نگاه میکند: بالا، پایین، چپ، یا راست. در زمان «$0$»، هر نینجا کونایِ خود را در جهتی که به آن سمت نگاه میکند پرتاب میکند.
هر کونای با سرعت «$1$» در جهت مستقیم حرکت میکند. اگر بیش از یک کونای در یک زمان به یک مکان بیایند، با هم برخورد میکنند و ناپدید میگردند. اندازهی کونای آنقدر کوچک است که میتوانیم از آن صرفنظر کنیم. همچنین، چون نینجاها میتوانند سریع حرکت کنند، مورد اصابت کونایها قرار نمیگیرند. هر کونای بدون از دستدادن سرعت در راستای خودش حرکتش را ادامه میدهد مگر اینکه با کونای دیگری برخورد کرده باشد.
در شکلهای زیر، پیکانها نمایشگر کونایها هستند. جهت هر پیکان جهت کونای متناظرش را نشان میدهد. در این شکلها، همهی پیکانهای پررنگ دچار برخورد میشوند.
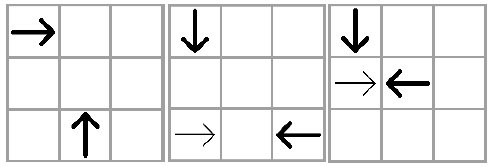
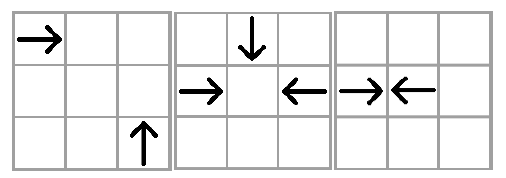 از طرف دیگر، در هر یک از شکلهای زیر، یک پیکان پررنگ هست که با پیکان پررنگ دیگر برخورد نمیکند. در شکل دوم و سوم، یک پیکان کمرنگ با یک پیکان پررنگ برخورد میکند. چون پیکانهای برخوردکرده ناپدید میشوند، یک پیکان پررنگ هست که با پیکان پررنگ دیگر برخورد نمیکند.
از طرف دیگر، در هر یک از شکلهای زیر، یک پیکان پررنگ هست که با پیکان پررنگ دیگر برخورد نمیکند. در شکل دوم و سوم، یک پیکان کمرنگ با یک پیکان پررنگ برخورد میکند. چون پیکانهای برخوردکرده ناپدید میشوند، یک پیکان پررنگ هست که با پیکان پررنگ دیگر برخورد نمیکند.
 تعداد خانههایی از جدول $W\times H$ را بشمارید که پس از گذشت مقدار کافی از زمان، کونایی از آنها گذر میکند.
تعداد خانههایی از جدول $W\times H$ را بشمارید که پس از گذشت مقدار کافی از زمان، کونایی از آنها گذر میکند.
ورودی
- خط اول ورودی شامل دو عدد صحیح $W$ و $H$ با فاصله از هم میباشد که اندازهی جدول را مشخص میکنند.
- خط دوم ورودی تنها شامل عدد صحیح $N$ است.
- خط $i$اُم ($1 \leq i \leq N$) از $N$ خط بعد، شامل سه عدد صحیح $X_i$، $Y_i$ و $D_i$ با فاصله از هم میباشد که نشان میدهد مکان نینجای $i$اُم در ستون $X_i$اُم از چپ و سطر $Y_i$اُم از بالای جدول است. هیچ دو نینجایی در یک مکان مشترک نیستند. جهت نینجای $i$ اُم با مقدار $D_i$ مشخص میشود.
- وقتی $D_i=0$، نینجای $i$اُم به سمت راست نگاه میکند.
- وقتی $D_i=1$، نینجای $i$اُم به سمت بالا نگاه میکند.
- وقتی $D_i=2$، نینجای $i$اُم به سمت چپ نگاه میکند.
- وقتی $D_i=3$، نینجای $i$اُم به سمت پایین نگاه میکند.
- تعداد نینجاها$1 \leq N \leq 10^5$
- اندازهی جدول$1 \leq H, W \leq 10^9$
- مختصات نینجاها $1 \leq X_i \leq W$,$1 \leq Y_i \leq H$
- در ۱۰ درصد تستها $W, H, N \leq 1000$.
- در ۴۰ درصد تستها $N \leq 1000$.
خروجی
در خروجی، تعداد خانههایی از جدول $W \times H$ را بنویسید که پس از گذشت مقدار کافی از زمان، کونایی از آنها گذر میکند.
محدودیتها
- محدودیت زمان: ۳ ثانیه
- محدودیت حافظه: ۲۵۶ مگابایت
ورودی و خروجی نمونه
| ورودی نمونه | خروجی نمونه |
|---|---|
| 5 4 5 3 3 2 3 2 0 4 2 2 5 4 1 1 1 3 | 11 |
| 7 6 12 3 2 3 6 3 2 7 1 3 1 5 0 3 6 1 6 6 1 4 5 2 1 3 0 6 5 2 5 1 2 6 4 3 4 1 3 | 29 |
توضیحات
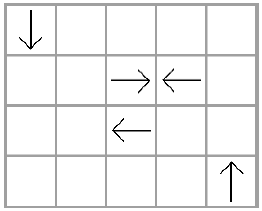
در نمونهی اول، وضعیت جدول در زمان «$0$» مانند شکل زیر است.
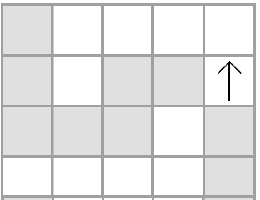
کونایِ پرتابشده توسط نینجای $i$اُم را کونای $i$اُم مینامیم. در زمان «$0.5$»، کونایِ ۲ و کونای ۳ با همدیگر برخورد کرده و ناپدید میشوند. شکل زیر وضعیت جدول را در زمان «$1$» نشان میدهد. در اینجا، خانههای خاکستری خانههایی را نشان میدهند که قبلاً از آنها کونای گذر کرده است.
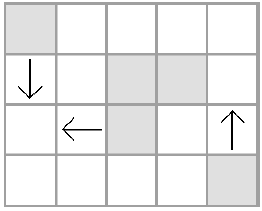 در زمان «$2$»، کونایِ ۱ و کونایِ ۵ با همدیگر برخورد میکنند و ناپدید میشوند. وضعیت جدول در زمان «$2$» در شکل زیر نشان داده شده است.
در زمان «$2$»، کونایِ ۱ و کونایِ ۵ با همدیگر برخورد میکنند و ناپدید میشوند. وضعیت جدول در زمان «$2$» در شکل زیر نشان داده شده است.
پس از زمان «$2$»، کوناهایِ دیگری در جایی از جدول با هم برخورد نمیکنند. وضعیت جدول پس از گذشت مقدار کافی از زمان مانند شکل زیر است.
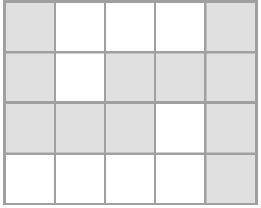 در نهایت، تعداد خانههایی از جدول که کونایی از آنها گذر میکند، ۱۱ است. پس باید «$11$» خروجی داده شود.
در نهایت، تعداد خانههایی از جدول که کونایی از آنها گذر میکند، ۱۱ است. پس باید «$11$» خروجی داده شود.