فهرست مندرجات
گرافهای قویا همبند
تعریف
جفت راس قویا همبند
در گراف جهتدار دو راس $u$ و $v$ قویا همبند هستند، اگر مسیری از $u$ به $v$ و مسیری از $v$ به $u$ وجود داشته باشد.
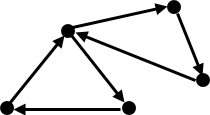
گراف قویا همبند
یک گراف جهت دار قویا همبند است اگر هر دو راس آن قویا همبند باشند. در تصویر میتوانید یک گراف قویا همبند را مشاهده کنید.
مؤلفهی قویا همبند
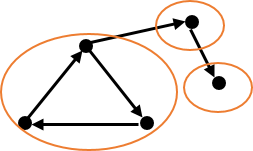 اگر یک زیر مجموعهای از رئوس گراف جهتدار $G$ همراه با تمام یالهای بین آنها(یک زیر گراف) که خاصیت قویا همبندی بین هر دو راس آن وجود دارد، قابل گسترش نباشد، یک مؤلفهی قویا همبند در گراف جهتدار $G$ است. قابل گسترش نبودن به این معنی که نتوان هیچ راسی به این زیرمجموعه اضافه کرد که همچنان این زیرمجموعه خاصیت قویا همبندی خود را حفظ کند. رئوس هر گراف جهتداری را میتوان به تعدادی مؤلفهی قویا همبند افراز کرد. (نمونه روبرو را ببنید)
اگر یک زیر مجموعهای از رئوس گراف جهتدار $G$ همراه با تمام یالهای بین آنها(یک زیر گراف) که خاصیت قویا همبندی بین هر دو راس آن وجود دارد، قابل گسترش نباشد، یک مؤلفهی قویا همبند در گراف جهتدار $G$ است. قابل گسترش نبودن به این معنی که نتوان هیچ راسی به این زیرمجموعه اضافه کرد که همچنان این زیرمجموعه خاصیت قویا همبندی خود را حفظ کند. رئوس هر گراف جهتداری را میتوان به تعدادی مؤلفهی قویا همبند افراز کرد. (نمونه روبرو را ببنید)
گراف معکوس
گراف معکوس، گرافی است که برای گرافهای جهتدار تعریف میشود. گراف $G=(V,E)$ مفروض است. مجموعهی $E'$ را از روی مجموعهی یالهای گراف $G$ به این صورت تعریف میکنیم: $$E'=\{ (u,v) | (v,u) \in E \} $$ گراف معکوس $G$ گرافیست با مجموعه راسی برابر با مجموعه راسی خود گراف $G$ و مجموعه یالی $E'$ . به عبارت سادهتر گراف معکوس $G$، همان گراف $G$ است که جهت یالهایش عکس شده.
$=(V,E')$ گراف معکوس $G$
ویژگی قویا همبندی بین هر دو جفت راس بعد از معکوس کردن حفظ میشود. (مسیر $u$ به $v$ حالا مسیر $v$ به $u$ است و برعکس). پس ویژگی قویاهمبندی گراف در گراف معکوس نیز حفظ میشود. به صورت کلیتر مولفههای قویا همبند گراف و گراف معکوس یکیست.

