فهرست مندرجات
ساخت تور اویلری به کمک DFS
تعریف
طبق تعریف تور اویلری، گراف G بدون جهت با حداکثر دو رأس درجه فرد داده شده است. حال به کمک DFS الگوریتمی را برای یافتن تور اویلری در آن معرفی میکنیم.
الگوریتم
در گراف جهت G داده شده، جهت پیدا کردن تور اویلری به کمک پیمایش نخست ژرفا DFS به این صورت عمل میکنیم که یک دنباله و پشتهی خالی در نظر میگیریم و؛
۱) اگر گراف رأس با درجه فرد نداشته باشد از رأسی دلخواه شروع میکنیم.
۲) اگر گراف دو رأس با درجه فرد داشته باشد از یکی از آن دو رأس شروع میکنیم.
۳) سایر گرافها تور اویلری ندارند.
هر بار رأس مورد نظر را بررسی میکنیم و اگر یالی از آن باقی نمانده بود آن را به تور اضافه میکنیم و رأس ابتدایی پشته را به عنوان رأس کنونی بعدی در نظر میگیریم، در غیر این صورت آن را در پشته اضافه میکنیم و یکی از همسایههایش را به عنوان رأس کنونی انتخاب میکنیم و یال میان آن دو را پاک میکنیم.
این کار را آنقدر ادامه میدهیم تا به رأسی بدون همسایه برسیم و پشته نیز خالی باشد. آنگاه دنباله رئوسی که ذخیره کردیم یک تور اویلری را تشکیل میدهند.
مراحل اجرایی:
۱- رأسی با درجه فرد و یا رأسی دلخواه را به عنوان رأس کنونی انتخاب میکنیم.
۲- اگر رأس کنونی همسایهای نداشت برو به ۴.
۳- یک یال متصل به رأس کنونی را پاک میکنیم.
۴- رأس کنونی را به پشته اضافه میکنیم و همسایه منتخب آن را به عنوان رأس کنونی قرار میدهیم و برو به ۲.
۵- رأس کنونی را به دنباله اضافه میکنیم.
۶- اگر پشته خالی بود برو به ۸.
۷- رأس ابتدایی پشته را به عنوان رأس کنونی انتخاب میکنیم و برو به ۲.
۸- پایان.
پیچیدگی الگوریتم
الگوریتم تنها از یک DFS استفاده میکند و در هر بازگشت در مسیر DFS یکی از رئوس گراف حذف میشود. بنابرین نتیجه میشود پیچیدگی الگوریتم از (O(V + E میباشد.
پیادهسازی اولیه
- A.c
#inlcude<iostream> #include<vector> #include<map> using namespace std; const int max_nodes = 100, max_edges; vector<pair<int, int> > adj[max_nodes]; vector<int> stack; bool seen[max_edges]; void dfs(int node){ int next = -1; for(int i = 0; i < adj[node].length(); i++){ int edge = adj[node][i]; if(!seen[edge.second]]){ seen[edge.second] = true; stack.push_back(node); dfs(edge.first); could_exit = true; break; } } if(!could_exit){ cout<< node <<endl; } } int main(){ int n, m; cin>> n>> m; for(int i = 0; i < m; i++){ int x, y; cin>> x>> y; x--; y--; adj[x].push_back(make_pair(y, i)); adj[y].push_back(make_pair(x, i)); } int odd_node = -1; for(int i=0; i<n ;i++){ if(adj[i].length()%2){ odd_node = i; } } trail(odd_node==-1?0: odd_node); }
کابردها
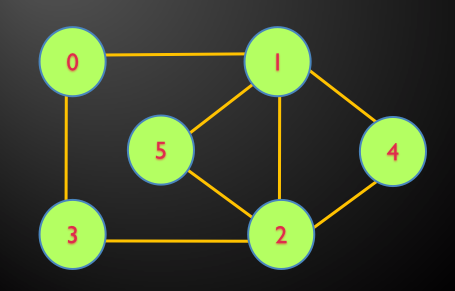
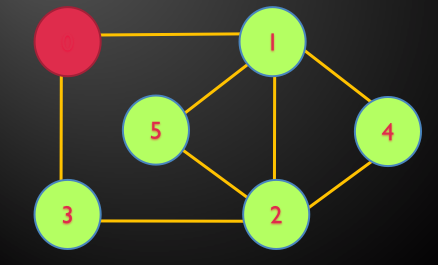
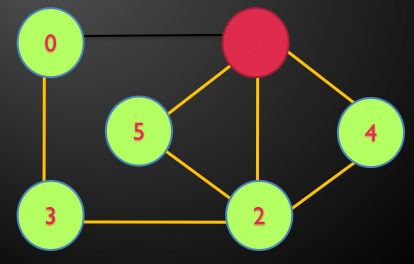
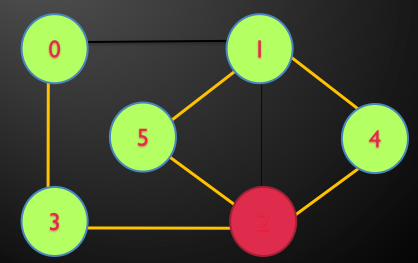
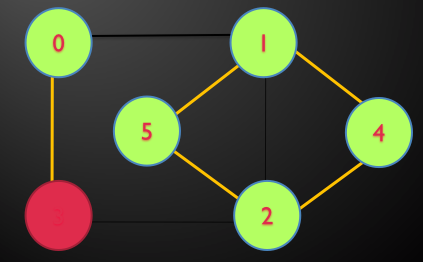
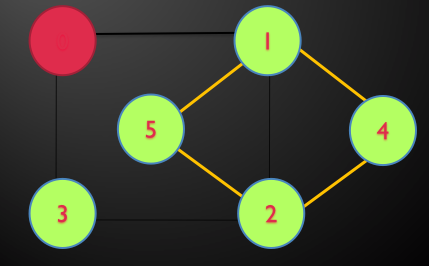
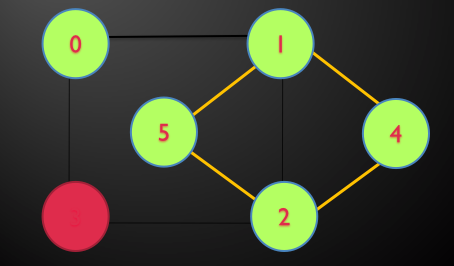
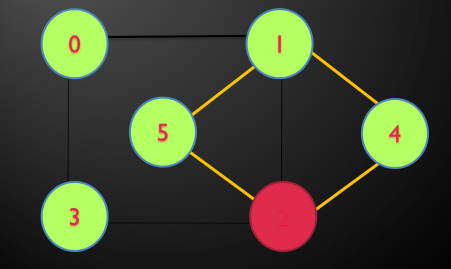
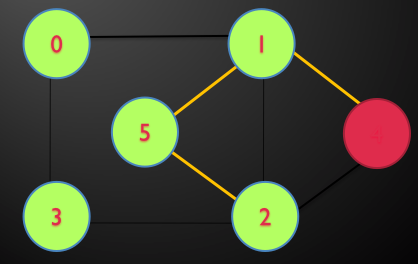
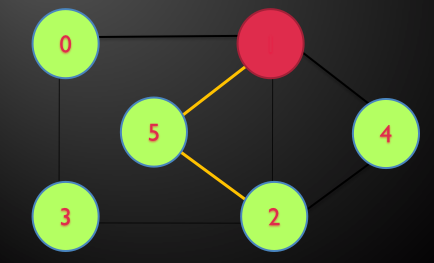
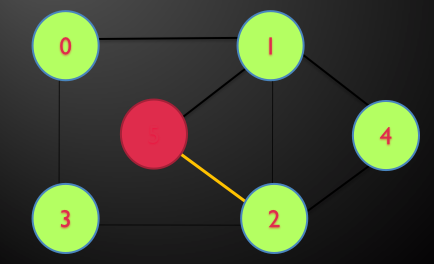
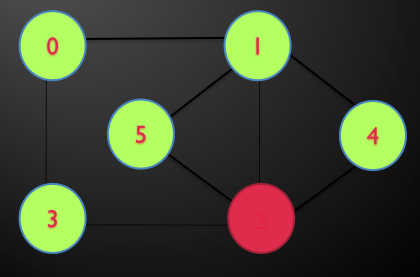
مثال: در گراف زیر توسط DFS تور اویلری را بیابید.