المپدیا

درخت کی دی

درخت کی دی نوعی ساختمان داده است که برای نگه داری نقطه ها در فضای k-بعدی استفاده می شود.درخت کی دی نوعی درخت دودویی است. در واقع می توان گفت این داده ساختار این قبلیت را دارد که بخشی متناهی از یک فضای k-بعدی را ذخیره کند.

نحوه ی ساخت

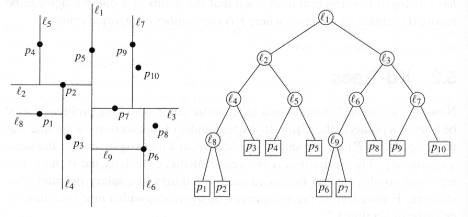
نقاط ورودی داده ساختار نقاطی در فضای k-بعدی هستند. هر راس از درخت کی دی یک نقطهٔ k-بعدی است و هر راس غیر برگ را می توان یک ابر صفحه در نظر گرفت که فضا را به دو قسمت تقسیم می کند و دو راسی که فرزند این راس هستنند نماینده آن بخش از فضا به حساب می آیند.

برای مثال اگر صفحه ی دوبعدی را درنظر بگیریم و یک خط x=3 را به عنوان جدا کننده در نظر بگیریم نقاط سمت چپ آن به عنوان فرزند سمت چپ این راس در نظر گرفته می شوند و نقاط سمت راست به عنوان فرزند سمت راست آن در نظر گرفته می شوند.

 
function build_kdtree (list of points pointList, int depth)
{
    // Select axis based on depth so that axis cycles through all valid values
    var int axis := depth mod k;
 
    // Sort point list and choose median as pivot element
    select median by axis from pointList;
 
    // Create node and construct subtree
    node.location := median;
    node.leftChild := kdtree(points in pointList before median, depth+1);
    node.rightChild := kdtree(points in pointList after median, depth+1);
    return node;
}

عملیات ها

• جست و جو : برای پیدا کردن یک عنصر در این درخت به مانند هر درخت دودویی دیگری در هر راسی که قرار داریم با بررسی این که راسی که به دنبال آن هستیم در چپ این راس یا در راست این راس قرار می گیرد به آن راس بروم وجست و جو را ادامه دهیم و چون ارتفاع درخت $logn$ است پس این کار در $O(logn)$ انجام می شود.

• حذف : برای حذف نیز به مانند درخت دودویی با پیدا کردن آن راس در $O(logn)$ سپس آن را حذف می کنیم که در محموع از $O(logn)$ می شود.

• درج :‌ به مانند جست و جو به از ریشه حرکت می کنیم و هنگام رسیدن به یک راس برسی می کنیم که آیا این راس در سمت راست آن باید قرار بگیرد یا در سمت چپ آن باید قرار بگیرد. این کار را تا رسیدن به آخرین راس ادامه می دهیم و از آن جا که ارتفاع درخت $logn$ است این کار در $O(logn)$ امکان پذیر است.