المپدیا

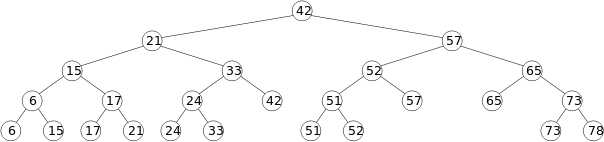
درخت محدوده‌ای

درخت محدوده‌ای داده‌ساختاریست که نقاط $k$-بعدی را ذخیره ‌می‌کند و نقاط درون یک بازه را بطور بهینه می‌توان از آن بدست آورد. این درخت جایگزین درخت کی‌دی است، با این تفاوت که جستجوی آن $O(nlog^dn)$ است که با استفاده از روش انتشار آبشاری می‌توان یک توان از عبارت $logn$ کم کرد و در نتیجه جستجوی‌ آن سریع‌تر است. ولی حافظه مصرفی آن بیشتر است و از مرتبه زمان جستجوی آن است.

درخت محدوده‌ای یک بعدی

درخت محدوده‌ای یک بعدی، همان درخت جستجوی دودویی متوازن است. تمامی عملیات‌ها روی این درخت $O(logn)$ هستند. این درخت برای مساله پیدا کردن تعداد نقاط در یک بازه مفید است.

درخت محدوده‌ای دو بعدی

این درخت برای حل مساله‌ پیداکردن تعداد نقاط در یک مستطیل بکار می‌رود. برای ساخت این درخت یک درخت محدوده‌ای یک بعدی روی بعد اول می‌سازیم، سپس هر راس از آن یک درخت‌ محدوده‌ای یک بعدی روی بعد دوم می‌شود. برای حل مساله گفته شده، ابتدا راس‌هایی که مقدار بعد اولشان درون مستطیل است را می‌یابیم و درون درخت‌ محدوده‌ای های روی بعد دوم آن ها بدنبال نقاط درون مستطیل می‌گردیم.

مقایسه درخت محدوده‌ای دو-بعدی و درخت کی‌دی دو-بعدی

درخت کی‌دی

• فضا $O(n)$
• زمان جستجو $O(k+sqrt(n))$
• زمان درج $O(logn)$

درخت محدوده‌ای

• فضا $O(nlogn)$
• زمان جستجو $O(k+log^2n)$
• زمان درج $O(log^2n)$

درخت محدوده‌ای در ابعاد بالاتر

همانند روشی که از یک بعد به دو بعد رسیدم، بعدهای بالاتر را نیز می‌توان ساخت. درواقع درخت محدوده‌ای d-بعدی، براساس بعد اول نقاط یک درخت محدوده‌ای یک-بعدی است که هر راس آن با توجه به بقیه ابعاد نقاط یک درخت محدوده‌ای d-1-بعدی است.

• زمان جستجو $O(k+log^dn)$

روش انتشار آبشاری به بهبود زمان جستجوی این درخت کمک می‌کند.