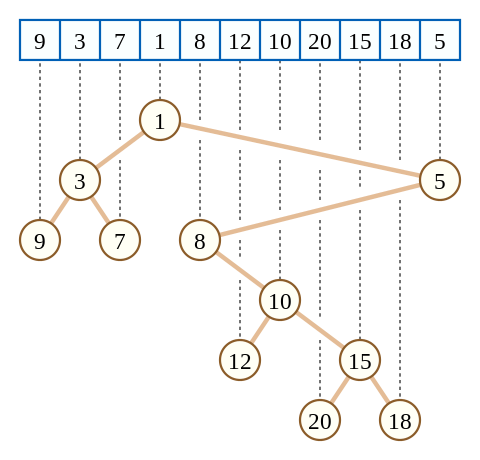
درخت دکارتی
درخت دکارتی روی یک آرایه از اعداد به این صورت تعریف میشود که هر عضو آرایه به یک راس در درخت تبدیل میشود. خروجی پیمایش In-Order درخت دکارتی باید آرایه اصلی باشد. همچنین درخت دکارتی باید خاصیت هرم کمینه را داشته باشد. این درخت روی هر آرایهای یکتا است. در تعریف داده ساختارهای treap و randomized binary search tree از درخت دکارتی به منظور جستجوی دودویی استفاده میشود.
نحوه ساخت درخت دکارتی
داده ساختارهای زیادی وجود دارند(مثلا درخت پارهخطی) که اگر آرایهمان را درون آنها ذخیره کنیم، میتوانیم در $O(logn)$ مقدار کمینه هر بازهای را بدست آوریم. برای ساخت یک درخت دکارتی از یکی از اینها استفاده میکنیم. ابتدا مقدار مینیمم کل آرایه را پیدا میکنیم و بهعنوان ریشه درخت دکارتی قرار میدهیم. سپس به طور بازگشتی درخت دکارتی عناصر سمت چپ و راست مقدار مینیمم را پیدا میکنیم. درخت دکارتی سمت چپ را بهعنوان فرزند چپ ریشه و درخت دکارتی سمت راست را به عنوان فرزند راست ریشه قرار میدهیم.
node get_root_cartesian_tree(int left, int right) { int min_index = get_min(left, right); node left_tree = get_root_cartesian_tree(left, min_index); node right_tree = get_root_cartesian_tree(min_index, right); node root; root.value = array[min_index]; root.left_child = left_tree; root.right_child = right_tree; return root; }
با این روش درخت دکارتی برای آرایهای از $n$ عنصر در $O(n.logn)$ ساخته میشود.
کاربردهای درخت دکارتی
یکی از کاربردهای درخت دکارتی در تبدیل مساله RMQ به مساله LCA است. به این شکل که برای حل مساله RMQ میتوانیم Cartesian Tree متناظر با آرایه را بسازیم، سپس مقدار کمینه یک بازه در آرایه به کوچکترین جد مشترک رئوس متناظر دو سر بازه در درخت دکارتی تبدیل میشود.